Deep Learning 1 - Develop a logic gate by perceptron

The perceptron is an algorithm that signals information from an input layer to an output layer. The figure shows the 2 inputs perceptron.

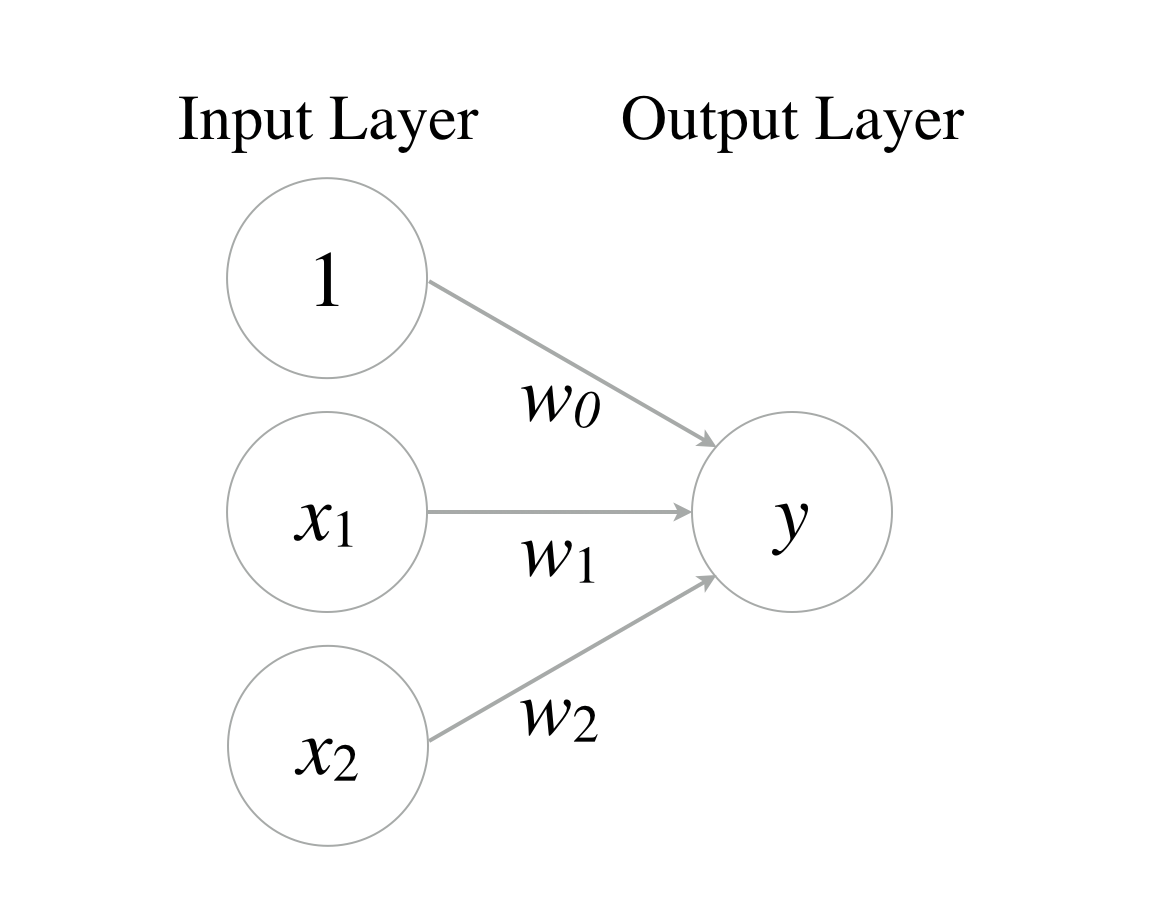
perceptron

are input signals, is an output signal, is a bias, and are weights. Signals are also called neurons or nodes. They output 1, only if the sum of inputs is over thresholds. In this case, the function is represented as follows:

You can create a logic gate with this function. If , , and , it will be the AND gate. This is the truth table for AND, OR, and NAND. Check the values () for the OR and NAND gates by yourself!

AND OR NAND
           
0    0    0 0    0    0 0    0    1
1    0    0 1    0    0 1    0    1
0    1    0 0    1    0 0    1    1
1    1    1 1    1    1 1    1    0

It is really simple. You can implement it with the following python code:

import numpy as np


def AND(x1, x2):
    x = np.array([1, x1, x2])
    w = np.array([-1.5, 1, 1])
    y = np.sum(w*x)
    if y <= 0:
        return 0
    else:
        return 1

def OR(x1, x2):
    x = np.array([1, x1, x2])
    w = np.array([-0.5, 1, 1])
    y = np.sum(w*x)
    if y <= 0:
        return 0
    else:
        return 1

def NAND(x1, x2):
    x = np.array([1, x1, x2])
    w = np.array([1.5, -1, -1])
    y = np.sum(w*x)
    if y <= 0:
        return 0
    else:
        return 1


if __name__ == '__main__':
    input = [(0, 0), (1, 0), (0, 1), (1, 1)]

    print("AND")
    for x in input:
        y = AND(x[0], x[1])
        print(str(x) + " -> " + str(y))

    print("OR")
    for x in input:
        y = OR(x[0], x[1])
        print(str(x) + " -> " + str(y))

    print("NAND")
    for x in input:
        y = NAND(x[0], x[1])
        print(str(x) + " -> " + str(y))

The results are here:

AND
(0, 0) -> 0
(1, 0) -> 0
(0, 1) -> 0
(1, 1) -> 1
OR
(0, 0) -> 0
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 1
NAND
(0, 0) -> 1
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 0

This is the first step to understand deep learning.

The sample code is here.

Reference

Related Posts