Deep Learning 6 - Calculate a value of the loss function

From this post, we’ll challenge learning process of neural network. The learning step is as follows;

  1. Divide a dataset into training data and test data
  2. Select part of training data (mini-batch) randomly
  3. Calculate the gradient to reduce the value of the loss function
  4. Update weights with the gradient
  5. Iterate step 2, 3, and 4

Before you implement them, you need to understand a loss function. It shows inaccuracy of neural networks. This procedure is the way to find parameters whose loss function will be minimal.

One of useful loss functions is cross-entropy error that is represented by;

Where is an output of neural network and is an answer label with a one-hot array (e.g. 7 -> [0,0,0,0,0,0,0,1,0,0]). It calculates the natural logarithm for the output related to the answer. As the output with the answer increase, the loss function gets closer to 0.

loss

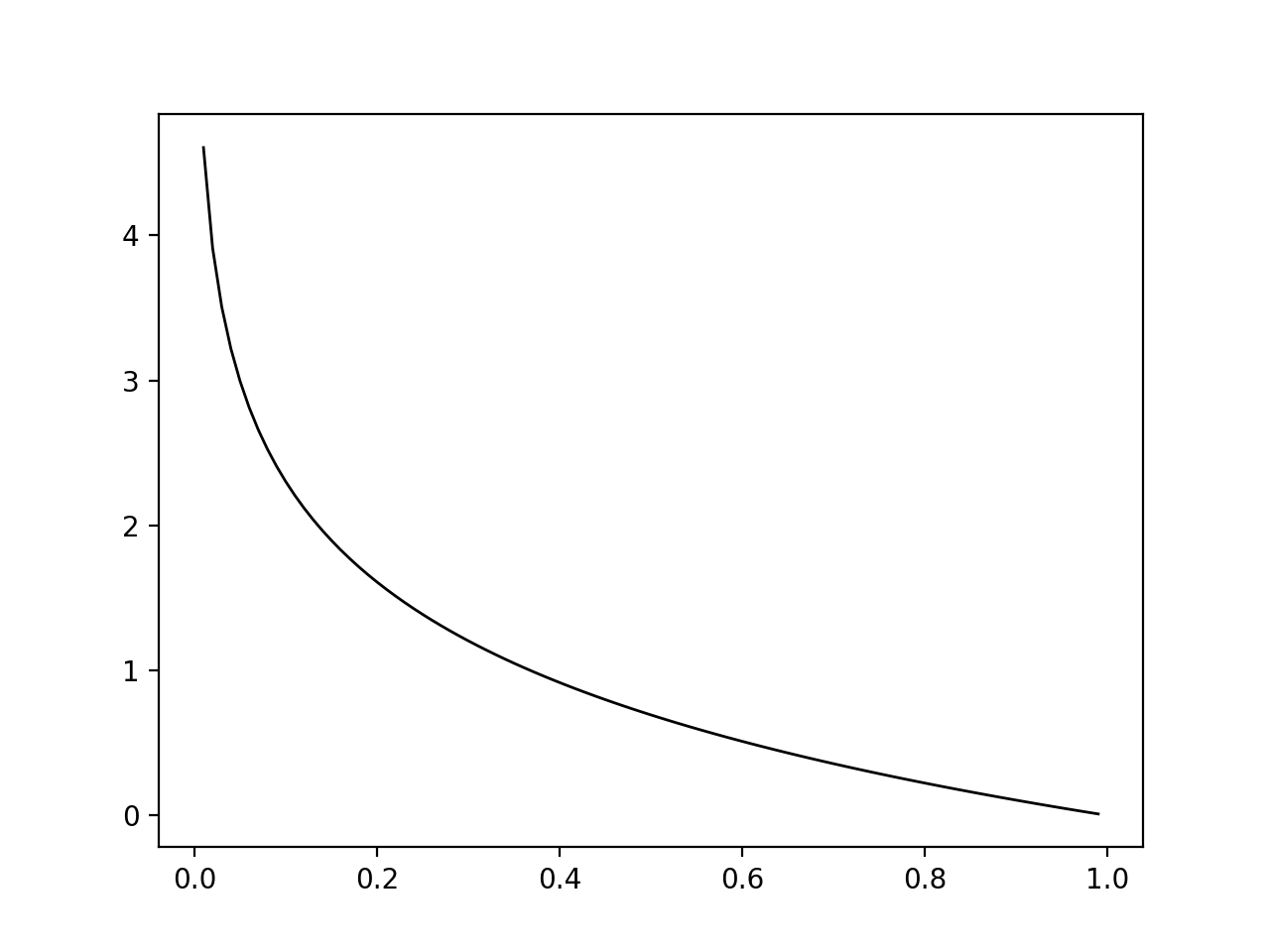
We’ve considered the loss function of one data. When you calculate the sum of data, the equation is simply transformed to;

However, it takes a lot of time to calculate it in practice. We usually handle it with a mini-batch that is randomly selected in the dataset.

06_loss.py
# Display all arrays
# np.set_printoptions(threshold=np.inf)

# Generate a mini-batch
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = x_train.shape[0]
batch_size = 3
batch_mask = np.random.choice(train_size, batch_size)
print(x_train[batch_mask])
print(t_train[batch_mask])

The result is here (If you want to see the all arrays, please insert np.set_printoptions);

[[ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]]
[[ 0.  0.  0.  0.  0.  0.  1.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.  1.  0.]
 [ 0.  0.  0.  1.  0.  0.  0.  0.  0.  0.]]

The following code is to calculate a value of the loss function with an answer label (not a one-hot array) when the outputs are bundled by mini-batch.

functions.py
def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

    # If t is a one-hot array, transform it into the answer label
    if t.size == y.size:
        t = t.argmax(axis=1)

    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t])) / batch_size

If you understand the loss function with a mini-batch, let’s go to the next step about the gradient!

The sample code is here.

Reference

Related Posts