Deep Learning 4 - Recognize the handwritten digit

If you’ve read my deep learning posts, you could learn a perceptron, an activation function, and the MNIST dataset. Now, you can understand a multiple neural network.

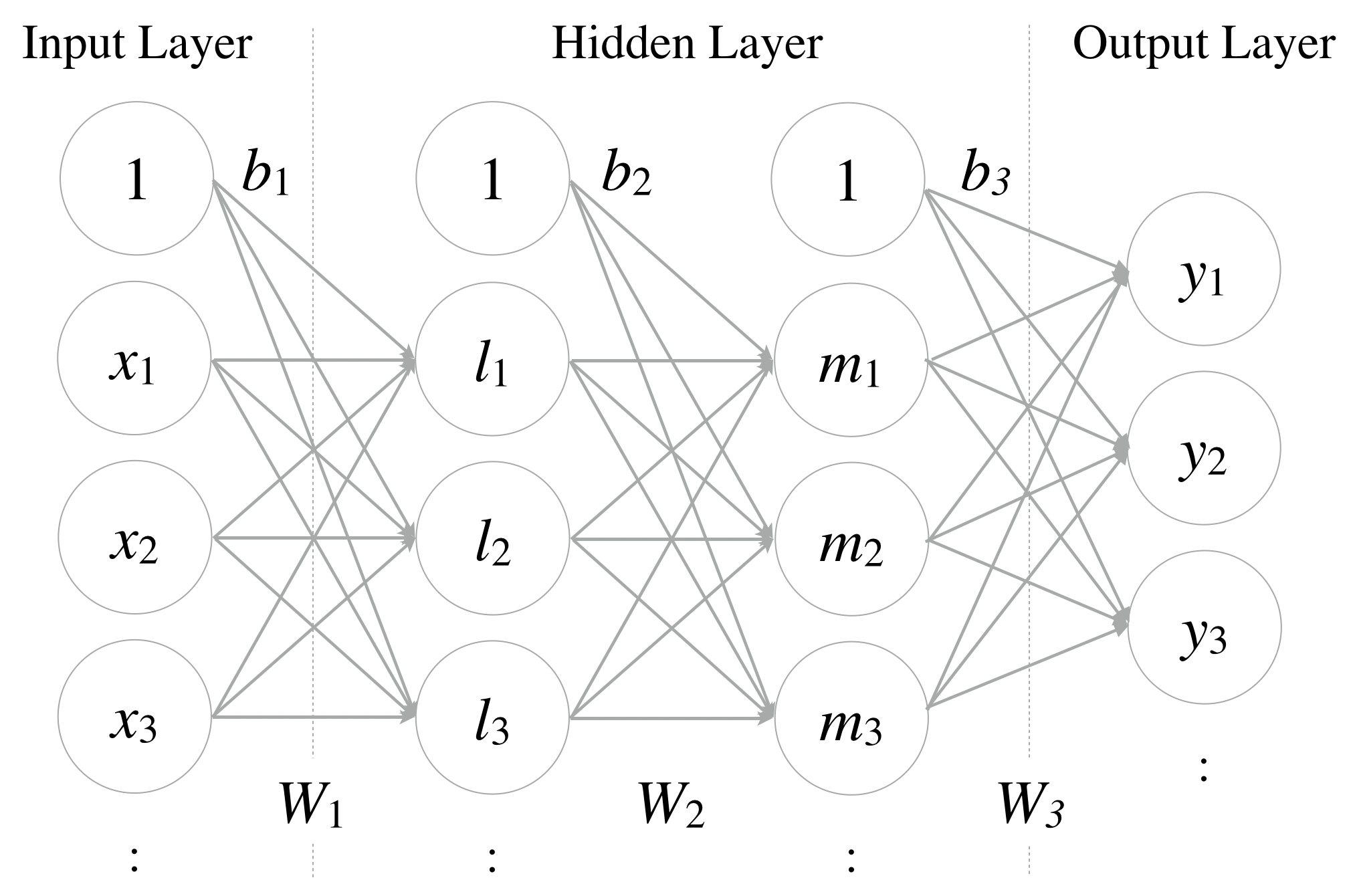
neural-network

This is a 3-layer neural network. Input layer and output layer are same as a perceptron, and there are 2 hidden layers. Each neuron is connected across adjacent layers, but not within a layer.

Let’s calculate accuracy for recognition of the MNIST dataset by using this network. The steps are as follows:

  1. Get the MNIST dataset
  2. Set the weight with sample_weight.pkl
  3. Transfer the information from input layer to output layer
  4. Calculate the accuracy
04_recognition.py
import os
import numpy as np
import pickle
from mnist import load_mnist
from functions import sigmoid, softmax


def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test

def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network

def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    l = sigmoid(np.dot(x, W1) + b1)
    m = sigmoid(np.dot(l, W2) + b2)
    y = softmax(np.dot(m, W3) + b3)

    return y


x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])
    p = np.argmax(y)
    if p == t[i]:
        accuracy_cnt += 1

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

There is a new activation function, softmax, in functions.py:

functions.py
import numpy as np

def softmax(x):
    x = x - np.max(x)
    return np.exp(x) / np.sum(np.exp(x))

As you can see, this function is expressed by the following equation:

The first one is the definition, and the second one is for calculation to prevent an overflow by exponential functions. The softmax function is often used in the final layer of neural networks.

If you execute it, you can get the accuracy. This is forward propagation of neural networks.

python 04_recognition.py
Accuracy:0.9352

You need to learn backward propagation to understand the learning process. Let’s move to the next step!

The sample code is here.

Reference

Related Posts